
Introduction – Noise measurements – Noise appearance – Noise summary
Scene-reference noise, SNR, and Dynamic Range – Temporal noise – ISO 15739 noise and SNR
Noise spectrum – Links
|
Dynamic Range – a general introduction with links to Imatest modules that calculate it. Multicharts/Multitest/eSFR ISO Noise – including chroma, sensor (RAW), and visual noise Temporal Noise – comparing the two-image and multi-image measurements |
Introduction
Noise is a random variation of image density, visible as grain in film and pixel level variations in digital images. It is a key image quality factor; nearly as important as sharpness. It is closely related to dynamic range— the range of brightness a camera can reproduce with reasonably good Signal-to-Noise Ratio (SNR) and contrast. Since it arises from basic physics— the photon nature of light and the thermal energy of heat— it will always be present. The good news is noise can be extremely low— often imperceptibly low— in digital cameras, particularly DSLRs with large pixels (4 microns square or larger). But noise can get ugly in compact digital cameras with tiny pixels, especially at high ISO speeds, and noise reduction software can have visible side-effects.
In most cases noise is perceived as a degradation in quality. But some Black & White photographers like its graphic effect: Many favored 35mm Tri-X film. (Film grain has very different statistics from digital noise— it’s multiplicative rather than additive, and its spectrum is dependent on density.) Pointillist painters, most notably George Seurat, created images from “noise” (specks of color) by hand; a task that can be accomplished in seconds today with Photoshop plugins. But by and large, the majority of photographers, especially color and large-format photographers, dislike noise with good reason. Noise is measured by several Imatest modules: Multicharts, Multitest, eSFR ISO, Colorcheck, Stepchart, and to a limited degree in SFR, SFRplus, and Uniformity. The first three modules— Multicharts, Multitest, and eSFR ISO— have the most comprehensive noise measurements.
Noise measurements typically refer to RMS (Root Mean Square) noise, which is identical to the standard deviation of the signal S.
RMS Noise = N =σ(S), where σ denotes the standard deviation.
S can be the signal in any one of several channels: R, G, B, Y (luminance, typically 0.2125 R + 0.7154 G + 0.0721 B), or a derived channel such as R-Y or B-Y (both used for chroma noise). L*, a*, b*, or others. See Multicharts/Multitest/eSFR ISO noise measurements.
Signal-to-Noise Ratio (SNR) is a measurement derived from noise that is often considered more important than noise itself. It is expressed as either a simple ratio (SNR = S/N) or in decibels, SNR(dB) = 20 log10(S/N), familiar to electrical engineers. In digital cameras noise consists of two parts: fixed noise (sensor dark current noise and thermal (resistive) noise) and shot (photon) noise, which increases with the square root of the mean number of photons striking the pixels.
Noise measurements
Noise measurements should ideally
- correlate with perceived appearance,
- (in many cases) be referenced to the original scene so the measurement is not affected by the tonal response (gamma, equivalent to contrast) of the camera or RAW converter,
- be detailed enough to allow accurate assessment of sensor and camera performance, and
- be simple enough to interpret without difficulty.
SNR— Since noise is only meaningful in relationship to a signal, a Signal-to Noise Ratio (SNR or S/N) is often calculated. SNR can be defined in many ways, depending on how Signal S is defined. For example, S can be an individual patch pixel level or the pixel difference corresponding to a specified scene density range (1.45 or 1.5 are often used for this purpose) or a low contrast object (for Contrast Resolution SNR). It is important to know precisely how SNR is defined whenever it is discussed. SNR can be expressed as a simple ratio (S/N) or in decibels (dB), where SNR (dB) = 20 log10(S/N). Doubling S/N corresponds to increasing SNR (dB) by 6.02 dB. Since these requirements can be somewhat contradictory, Imatest modules have several noise and SNR measurements, some simple and some detailed.
Multicharts, Multitest, Stepchart, and Colorcheck include the following noise displays:
- Noise a function of pixel level or exposure, expressed in
- Pixels, normalized to the pixel difference corresponding to a scene density range of 1.5 for Stepchart (comparable to the density range of 1.45 for the GretagMacbeth ColorChecker) or the White – Black zones in the ColorChecker (row 3, patches 1 – 6; density range = 1.45). Without this normalization, noise is a function of RAW converter response curve; it increases with converter contrast.
- Pixels, normalized to the maximum pixel value: 255 for 8/24-bit files.
- Pixels (maximum of 255 for 8/24-bit files)
- f-stops (or EV or zones; a factor of two in exposure), i.e., referenced to the original scene. Noise measured in f-stops corresponds closely to human vision. See f-stop noise, below.
- Noise as a simple (average) number
- A good single number for describing noise is the average noise of the Y (Luminance) channel, measured in pixels (normalized scene density difference of 1.5), shown in the lower plot in the figures, below. The lightest and darkest zones, representing chart densities greater than 1.5 or less than 0.1 are excluded from the average.
- S/N or SNR (dB) as a function of pixel level or exposure, where S is the pixel level of the individual test chart patch.
- S/N or SNR (dB) as a simple (average) number.
- A good single number for defining SNR is the White – Black SNR, SNR_BW, where S is the difference in pixel levels between the White and Black patches in the GretagMacbeth ColorChecker in Colorcheck (density range of 1.45), or the pixel difference corresponding to a chart (scene) density difference of 1.5 in Stepchart. Noise N is measured in a gray patch with density around 0.7. SNR_BW was developed to reduce the effect of image contrast (resulting from image processing, i.e., the application of a gamma curve) on the noise measurements.
\( SNR_{BW} = 20 log_{10}bigl( frac{S_{WHITE} – S_{BLACK}}{N_{MID}} bigr) \)
- A good single number for defining SNR is the White – Black SNR, SNR_BW, where S is the difference in pixel levels between the White and Black patches in the GretagMacbeth ColorChecker in Colorcheck (density range of 1.45), or the pixel difference corresponding to a chart (scene) density difference of 1.5 in Stepchart. Noise N is measured in a gray patch with density around 0.7. SNR_BW was developed to reduce the effect of image contrast (resulting from image processing, i.e., the application of a gamma curve) on the noise measurements.
- a noise spectrum plot, described below.
Uniformity displays a spatial map of noise.
Multicharts, Multitest, and eSFR ISO contain the most comprehensive noise analysis and displays. The various noise calculations (which include everything from Stepchart and Colorcheck) are listed in the following table (more are added from time to time).
| 1. | Noise vs. input density (RGB) Noise in pixels or % of maximum pixel level | 2. | Simple noise or SNR derived from standard deviation (σ) of pixel levels. |
| 2. | Signal/Noise (S/N) vs. input density (RGBY) The luminance (Y-channel) is used for S. | ||
| 3. | SNR (dB) vs. input density (RGBY) SNR (dB) = 20 log10(S/N). | ||
| 4. | Chroma noise vs. input density | 3. | Industry-standard chroma noise |
| 5. | Chroma S/N vs. input density | ||
| 6. | Chroma SNR (dB) vs. input density | ||
| 7. | CIELAB (L*a*b*) noise | 3. | Experimental: Seems to make sense since CIELAB is approximately perceptually uniform, but has no industry traction. |
| 8. | CIELAB (L*a*b*) S/N | ||
| 9. | CIELAB (L*a*b*) SNR (dB) | ||
| 10. | Noise vs. pixel (all patches) | 2. | For characterizing sensors from RAW (unprocessed or minimally processed) images. |
| 11. | S/N vs. pixel (all patches) | ||
| 12. | SNR (dB) vs. pixel (all patches) | ||
| 13. | F-stop (scene-referenced) noise, including Dynamic Range results. | 2. | Used for Dynamic Range calculations. Defined here. |
| 14. | Scene-referenced S/N (ratio), including Dynamic Range results. |
||
| 15. | Scene-referenced SNR (dB), including Dynamic Range results. | ||
| 16. | ISO 15739 Visual noise vs. input density (L*u*v*) | V. | From the ISO 15739:2013 standard. Includes viewing conditions. |
| 17. | ISO 15739 Visual S/N vs. input density (L*u*v*) | ||
| 18. | ISO 15739 Visual SNR (dB) vs. input density (L*u*v*) | ||
| 19. | ISO 15739 Noise and Dynamic Range |
2. | Also from ISO 15739:2013. Completely independent of visual noise. |
| 20. | ISO 15739 Signal/Noise (S/N) and Dynamic Range |
||
| 21. | ISO 15739 Signal-to-Noise Ratio (SNR) in dB |
||
| 22. | CPIQ Visual Noise (CIELAB) | V. | |
| 23. | CPIQ Visual S/N (CIELAB) | ||
| 24. | CPIQ Visual SNR (dB) (CIELAB) | ||
| 25. | YUV noise | 3. | |
| 26. | YUV S/N | ||
| 27. | YUV SNR (dB) |
The entry in the third column is from the Noise settings window: 1. No noise, 2. Elementary noise (fast calculations),
3. Advanced noise (slower), and V. Visual noise (separate settings for ISO and CPIQ visual noise).
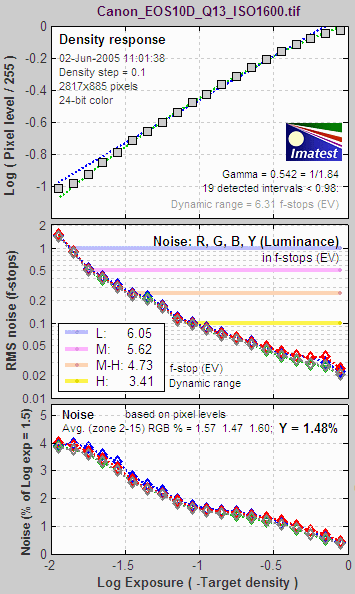
Noise appearanceThe appearance of noise is illustrated in the stepchart images on the right. Noise is usually measured as an RMS (root mean square) voltage. The mathematics of noise is presented in a green box at the bottom of this page. The stepcharts in columns (A)-(C) are simulated. They are assumed to have a minimum density of 0.05 and density steps of 0.1, identical to the Kodak Q-13 and Q-14. They have been encoded with gamma = 1/2.2 for optimum viewing at gamma = 2.2 (the Windows/Internet standard). Strong noise— more than you’d find in most digital cameras— has been added to columns (A) and (B). Column (C) is noiseless. The fourth column (D) contains an actual Q-13 stepchart image taken with the Canon EOS-10D at ISO 1600: a very ISO high speed. Noise is visible, but low for such a high ISO speed (thanks, no doubt, to software noise reduction). The noise in (A) is constant inside the sensor, i.e., before gamma encoding. When it is encoded with gamma = 1/2.2, contrast, and hence noise, is boosted in dark areas and reduced in light areas. The On Semiconductor publication, CCD Image Sensor Noise Sources, indicates that this is not a realistic case. Sensor noise tends to increase with brightness. The noise in (B) is uniform in the image file, i.e., its value measured in pixels is constant. This noise must therefore increase with brightness inside the sensor (prior to gamma encoding), and hence is closer to real sensor behaviour than (A). Noise appears relatively constant except for the darkest zones, where it’s not clearly visible. Noise is often lower in the lightest zones, where a tonal response “S” curve superimposed on the gamma curve (or saturation) reduces contrast, hence noise. For this reason the middle zones— where noise is most visible— are used to calculate the average noise: a single number used to characterize overall noise performance. We omit zones where the density of the original chart (hence display density in an unmanipulated image) is greater than 1.5 or less than 0.1. Characteristic Stepchart results are shown below. |
|
Column (B): Uniform pixel noiseThis image has simulated uniform pixel noise (i.e., constant noise in the image file, measured in pixels). The upper plot is the tonal response (or characteristic curve) of the camera. It shows the expected ideal response for encoding with gamma = 1/2.2 = 0.4545: a straight line with slope = 0.4545 for the log-log plot. The middle plot shows noise measured in f-stops (or EV or zones). Noise increases more steeply for dark regions (large negative values of Log Exposure) in actual sensors. The lower plot shows noise measured in pixel levels, normalized to the difference in pixel levels for a density range of 1.5. It is relatively constant, showing only statistical variation, except for the brightest level (on the right), where the noise is reduced because some samples are clipped at pixel level 255. The lower plot also contains the single number used to characterize overall noise performance: the average Luminance channel noise (Y = 5.59%, on the right near the top). This number is very high; it corresponds to poor image quality. This is SNR in dB for simulated uniform pixel noise. Because of the gamma = 2.2 encoding, SNR inproves by 6.02/2.2 = 2.74 dB for each doubling of exposure (0.301 density units); roughly 9.1 dB per decade (1 density unit). 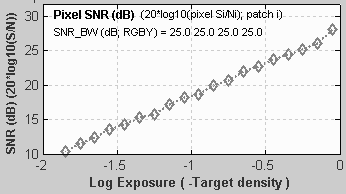 |
|
Column (D): Canon EOS-10D at ISO 1600Unlike the above figure (for the image in column (B)), real data for the Canon EOS-10D at ISO 1600 is used.The upper plot shows a slight tonal response “S” curve superimposed on the gamma curve (which is a straight line in this log-log plot). Some converter settings (such as “low contrast”) result in a much more pronounced “S” curve. The middle plot shows f-stop noise, which increases dramatically in the dark regions. The lower plot shows the normalized pixel noise. It increases in the dark regions. This increase is due in part to the high ISO speed. Digital cameras achieve high ISO speed by amplifying the sensor output, which boosts noise, particularly in dark regions. This curve looks different for the minimum ISO speed: noise values are much lower and subject to more statistical variation. This is SNR in dB for the Canon EOS-10D at ISO 1600. (This display option was introduced with Imatest 2.3.16). SNR improves by about 6 dB for each doubling of exposure (0.301 density units); roughly 20 dB per decade (1 density unit), which is what would be expected for constant sensor noise. (This curve would be dramatically different at lower ISO speeds.) 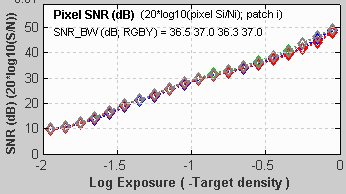 |
 |
Noise summary
There are two basic types of noise.
- Temporal. Noise which varies randomly each time an image is captured. Measured by Multicharts, Multitest, Colorcheck, and Stepchart using two identical input images for all modules or multiple images (4-16 with 8 recommended) for Multicharts and Multitest, as described in Measuring Temporal Noise.
- Spatial or fixed pattern. Noise caused by sensor nonuniformities. Sensor designers have greatly reduced fixed pattern noise in the last decade.
Temporal noise can be reduced by signal averaging, which involves summing N images, then dividing by N. This is an option for all Imatest analysis modules when several image files are selected (you can also analyze the individual files separately). Summing N individual images increases the summed signal pixel level (voltage) by N. But since temporal noise is uncorrelated, noise power (rather than voltage or pixel level) is summed. Since voltage is proportional to \(sqrt{text{power}}\), the noise pixel level (which is proportional to noise voltage) increases by \(sqrt{N}\). Signal-to-noise ratio (S/N or SNR) improves by \(N / sqrt{N} = sqrt{N}\). S/N is improved by a factor of 2 (6.01 dB) for 4 images, 4 for 16 images, etc.
Several factors affect noise.
- Pixel size. Simply put, the larger the pixel, the more photons reach it, and hence the better the signal-to-noise ratio (SNR) for a given exposure. The number of electrons generated by the photons is proportional to the sensor area (as well as the quantum efficiency). Noise power is also proportional to the sensor area, but noise voltage is proportional to the square root of power and hence area. If you double the linear dimensions of a pixel, you double the SNR. The electron capacity of a pixel is also proportional to its area. This directly affects dynamic range.
- Sensor technology and manufacturing. The biggest technology issue is CMOS vs. CCD. We won’t discuss it in detail here. Until 2000 CMOS was regarded as having worse noise, but it has improved to the point where the two technologies are comparable, differing only in detail. CMOS is less expensive because it is easy to add functionality to the sensor chip. Technology also involves other aspects of sensor design and manufacturing, all of which will improve gradually with time.
- ISO speed (Exposure Index) setting. Digital cameras control ISO speed by amplifying the signal (along with the noise) at the pixel. Hence, the higher the ISO speed the worse the noise. To fully characterize a sensor it must be tested at several ISO speeds, including the lowest and highest.
- Exposure time. Long exposures with dim light tend to be noisier than short exposures with bright light, i.e., reciprocity doesn’t work perfectly for noise. To fully characterize a sensor it should be tested at long exposure times (several seconds, at least).
- Digital processing. Sensors typically have 12-bit analog-to-digital (A-to-D) converters, so digitization noise isn’t usually an issue at the sensor level. But when an image is converted to an 8-bit (24-bit color) JPEG, noise increases slightly. The noise increase can be worse (“banding” can appear) if extensive image manipulation (dodging and burning) is required. Hence it is often best to convert to 16-bit (48-bit color) files. But the output file bit depth makes little difference in the measured noise of (unmanipulated) files.
- Raw conversion. Raw converters often apply noise reduction (lowpass filtering) and sharpening (see Noise frequency spectrum, below), whether you want it or not; even if NR and sharpening are turned off. This makes it difficult to measure the sensor’s intrinsic properties.
General comments
- Imatest subtracts gradual pixel level variations from the image before calculating noise (the standard deviation of pixel levels in the region under test). This removes errors that could be caused by uneven lighting. Nevertheless, you should take care to illuminate the target as evenly as possible.
- The target used for noise measurements should be smooth and uniform– grain (in film targets) or surface roughness (in reflective targets) should not be mistaken for sensor noise. Appropriate lighting (using more than one lamp) can minimize the effects of surface roughness.
F-stop noise, scene-referenced SNR, and Dynamic Range
F-stop noise and scene-referenced SNR
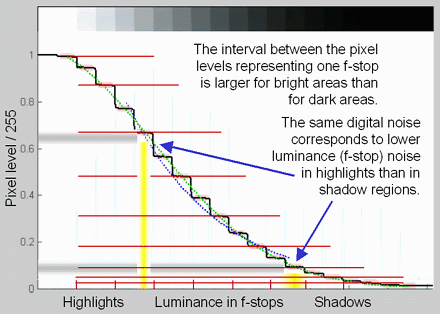
ΔL ≈ 0.01 L –or– ΔL/L ≈ 0.01 where ΔL is the smallest luminance difference the eye can distinguish. This equation is approximate; effective ΔL tends to be larger in dark areas of scenes and prints due to visual interference (flare light) from bright areas. Expressing noise in relative luminance units, such as f-stops, corresponds more closely to the eye’s response than standard pixel or voltage units. Noise in f-stops = Nf-stop is obtained by dividing the noise in pixels by the number of pixels per f-stop. (We use “f-stop” rather than “zone” or “EV” out of habit; any of them are OK.) Note that 1 f-stop = 0.301 Optical density units = 6.02dB (decibels) = log2(luminance). Also note that Nf-stop is scene-referenced noise in (logarithmic) units of f-stops, and must be distinguished from linear scene-referenced noise, Nscene-ref, which has the same linear units as luminance (the scene signal).
The above-right image illustrates how the pixel spacing between f-stops (and hence d(pixel)/d(f-stop)) decreases with decreasing brightness. This causes f-stop noise to increase with decreasing brightness, visible in the figures above. Since f-stop noise and scene-referenced SNR are functions of scene luminance, largely independent of image signal processing and fogging from flare light, they are an excellent indicators of real-world camera performance. They are the basis of Imatest Dynamic Range measurements.
|
Imatest has several types of Dynamic Range calculation, which are cross-referenced here.
| Dynamic range from a single transmissive chart image. | Stepchart, Multicharts, Mutitest | A transmissive chart is such as the Imatest 36-patch Dynamic Range or HDR chart is required because reflective charts do not have sufficient tonal range. |
| Dynamic range from multiple (differently exposed) images | Dynamic Range module | Uses CSV output of Stepchart of Multitest for several differently exposed images. Usually used with reflective charts, but transmissive charts may also be used. |
| ISO 15739 Dynamic Range from patch with density ≈ 2 | Multicharts, Multitest, eSFR ISO | Extrapolates Dynamic Range from a single patch with density ≈ 2. |
| Raw sensor Dynamic Range | Multicharts, Multitest | Fits raw data to an equation from the EMVA 1288 standard, then extrapolates to find DR. The test chart does not have to have as large a tonal range as the DR, but transmissive charts with tonal range ≥ 3 are recommended. |
Since scene-referenced noise and SNR are independent of the tonal response curve, they are used as the basis for Imatest Dynamic Range calculations, which are described elsewhere. Dynamic Range is the range of exposure (scene brightness) where quality exceeds a specified level, which we define as 20 dB for “high quality” down to 0 dB for “low quality”. Here is an illustration. The upper curve is the tonal response plot showing gamma. The lower plot is the scene-referenced noise, showing Dynamic Range at several quality levels.
 Tonal response and scene-referenced SNR for an image converted from raw with dcraw.
Tonal response and scene-referenced SNR for an image converted from raw with dcraw.
Temporal noise
Four Imatest modules— Multicharts, Multitest, Colorcheck, and Stepchart— can measure temporal noise— noise that varies independently from image to image, with fixed-pattern noise omitted. It can be calculated by two methods:
- the difference between two identical test chart images (the Imatest recommended method), and
- the ISO 15739-based method, which where it is calculated from the pixel difference between the average of N identical images (N ≥ 8) and each individual image (Multicharts and Multitest-only).
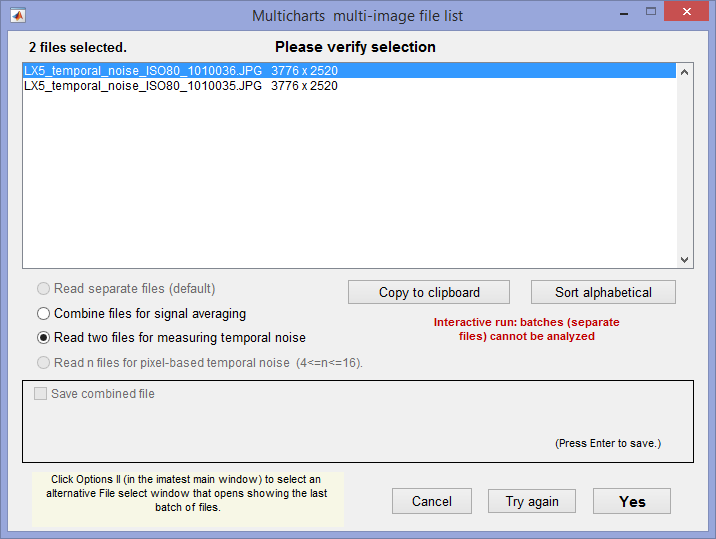
(1) Difference method. In any of the modules, read two images. The window shown on the right appears. Select the Read two files for measuring temporal noise radio button.
The two files will be read and their difference (which cancels fixed pattern noise) is taken. Since these images are independent, noise powers add. For indendent images I1 and I2, temporal noise is
\(displaystyle sigma_{temporal} = frac{sigma(I_1 – I_2)}{sqrt{2}}\)
In Multicharts and Multitest temporal noise is displayed as dotted lines in Noise analysis plots 1-3 (simple noise, S/N, and SNR (dB)).
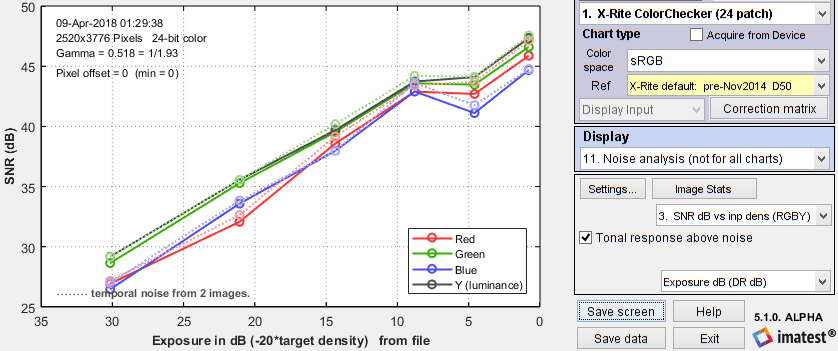 SNR (dB) for Colorchecker chart: temporal noise shown as thin dotted lines.
SNR (dB) for Colorchecker chart: temporal noise shown as thin dotted lines.
(2) Multiple file method. From ISO 15739, sections 6.2.4, and 6.2.5. Currently we are using simple noise (not yet scene-referred noise). Select between 4 and 16 files. In the multi-image file list window (shown above) select Read n files for temporal noise. Temporal noise is calculated for each pixel j using
\(displaystyle sigma_{diff}(j) = sqrt{frac{1}{N} sum_{i=1}^N (X_{j,i} – X_{AVG,j})^2} = sqrt{frac{1}{N} sum_{i=1}^N X_{j,i}^2 – left(frac{1}{N} sum_{i=1}^N X_{j,i}right)^2 } \)
The latter expression is used in the actual calculation since only two arrays, \(sum X_{j,i} text{ and } sum X_{j,i}^2 \), need to be saved. Since N is a relatively small number (between 4 and 16, with 8 recommended), it must be corrected using formulas from Identities and mathematical properties in the Wikipedia standard deviation page. \(s(X) = sqrt{frac{N}{N-1}} sqrt{E[(X – E(X))^2]}\).
\(sigma_{temporal} = sigma_{diff} sqrt{frac{N}{N-1}}\)
We currently recommend the difference method (1) because our experience so far has shown no advantage to method (2), which requires many more images (N ≥ 8 recommended), but allows fixed pattern noise to be calculated at the same time. There is a detailed comparison of the methods in Measuring Temporal Noise.
ISO 15739 noise and SNR
The updated ISO 15739:2013 standard has several definitions for noise, SNR, and Dynamic Range that are similar to f-stop noise, but with some important differences. The ISO definition of Signal-to-Noise Ratio (§6.2.3-6.2.5 and Annex D) is
\( SNR = Q = gL / sigma\)
where σ = noise in pixels, L = luminance (linear), and g is the first derivative of the OECF (pixel level vs. luminance curve).
\( g = d(text{pixel}) / dL\) Though it isn’t obvious from the standard, L must be scaled (multiplied) by Lref, as defined in §6.2.2. The numeric version this equation is given in Annex D.
When ISO 15739 SNR is displayed in Multicharts, Multitest, or eSFR ISO, it can be compared with the older Imatest f-stop-based calculation. Results are similar (though not identical).
| (Obsolete section: kept for reference) Definitions: Pxl = pixel level (same as OL = output level in the ISO standard.) σpx = noise in pixels (note: standard deviation σ is equivalent to RMS noise.) L = Illumination or exposure level. (Units will not be important.) f-stops = log2L f-stop noise = σfst = σpx /(d(Pxl)/d(f-stops)) = σpx /(d(Pxl)/d(log2L)) f-stop SNR = SNRfst = 1/σfst = (d(Pxl)/d(log2L)) / σpx We will apply the equation, d(logb(x))/dx = 1/(x ln(b)), where ln(2) = 0.6931 = 1/1.4427. Now, from the ISO standard, Incremental gain = gI = d(Pxl)/dL (Note linear units) = d(Pxl)/d(log2L) × d(log2L) / dL = 1.442(d(Pxl)/d(log2L)) / L Appendix D of the ISO 15739 standard defines total Signal-to-Noise Ratio as SNRISO = L gI / σpx = 1.4427 L (d(Pxl)/d(log2L)) / (L σpx) = 1.4427 (d(Pxl)/d(log2L))/σpx which leads to SNRISO = 1.4427 SNRfst SNRISO is larger than SNRfst by a factor of 1.4427, or equivalently, 3.18 dB. |
|
The mathematics of noise (just a taste) Amplitude distribution
|
Noise frequency spectrum
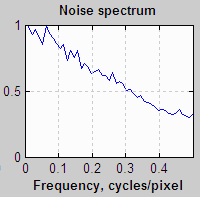
In addition to an amplitude distribution, noise is characterized by a frequency spectrum, calculated by taking the Fourier transform of the spatial image. The spectrum is closely related to appearance. Two spectra are shown below, taken from the second Stepchart figure. The first is for the image from column (B), above, which contains simulated white noise. The second is for the image in column (D), above, taken with the Canon EOS-10D at ISO 1600. The images shown below have been magnified 2X (using the nearest neighbor resizing algorithm) to emphasize the pixel distribution. They are close approximations to the images used to calculate the spectra (though not the exact images).
|
|
 |
 White noise, enlarged 2X (nearest neighbor) |
 Blurred noise, enlarged 2X (nearest neighbor) |
White noise (unfiltered electronic noise is white) has two key properties. 1. The values of neighboring pixels are uncorrelated, i.e., independent of one-another. 2. Its spectrum is flat. The white noise spectrum (above, left) shows statistical variation and a small peak at 0.25 cycles/pixel, probably caused when the image in column (B) was resized for display. For spectral (non-white) noise, neighboring pixels are correlated and the spectrum is not flat. The spectrum and image (above, right) are the result of blurring (also called smoothing or lowpass filtering), which can result from two causes
- The Bayer sensor demosaicing algorithm in the RAW converter causes the noise spectrum to drop by about half at the Nyquist frequency (0.5 cycles/pixel), and
- Noise reduction (NR) software lowpass filters noise, i.e., reduces high frequency components. With the widely-used bilateral filter (which can be simulated with the Image Processing module), NR uses a threshold that prevents portions of the image near contrast boundaries from blurring.
But NR comes at a price: detail with low contrast and high spatial frequencies can be lost. This causes the “plasticy” appearance sometimes visible on skin. Some people love it (plastic surgeons make a lot of income); I don’t This loss can be quantified with Imatest Log F-Contrast measurements.The visibility of noise depends on the noise spectrum, though the exact relationship is complex. Noise at high spatial frequencies may be invisible in small prints (low magnifications) but very damaging in large prints (large magnifications). Because of the complex nature of the relationship, Kodak established a subjective measurement of grain (i.e., noise) called Print Grain Index (Kodak Technical Publication E-58). Visual noise measurements are intended to predict the visual effect of noise, based on noise spectrum and viewing conditions.
Sharpening and unsharp masking (USM) are the inverse of blurring. They boost portions of the spectrum and cause neighboring pixels to become negatively correlated, i.e., they exaggerate the differences between pixels, making the image appear noisier. USM is often applied with a threshold that restricts sharpening to the vicinity of contrast boundaries. This prevents noise from degrading the appearance of smooth areas like skies. In images taken with poor quality lenses (or misfocused or shaken), the image is lowpass filtered (blurred) but the noise is not. Some sharpness loss can be recovered with sharpening or USM, but noise is boosted in the process. That’s why good lenses are important, even with digital sharpening.
Links
CCD Image Sensor Noise Sources (from On Semiconductor) An excellent, highly readable introduction to the different noise sources. Noise sources in CMOS sensors differ only in relative magnitude.
Neat Image is a remarkable program for reducing noise. Instead of lowpass filtering, the software is trained to recognize the structure of the noise. It can reduce noise with minimal side-effects. Particularly valuable at high ISO speeds.
EMVA 1288 Standard contains an excellent, well-written introduction to the mathematics of noise.
Photography — Electronic still-picture imaging — Noise measurements (ISO 15739:2003) Somewhat difficult to read, but it’s the official standard. Its Dynamic Range measurement is extrapolated from measurements from a black reference density of 2.0.






 In most cases, the pixel or density variations that comprise noise can be modeled by the
In most cases, the pixel or density variations that comprise noise can be modeled by the