A comparison of sensitivity to signal processing
In this page we address concerns about the sensitivity of slanted-edge patterns to signal processing, especially sharpening, and we correct the misconception that sinusoidal patterns, such as the Siemens star, are insensitive to sharpening, and hence provide more robust and stable MTF measurements. The Siemens Star is of particular interest because, along with the slanted-edge, it is included in the ISO 12233:2014 standard.
To summarize our results, we found that sinusoidal patterns are sensitive to sharpening, though often less so than low contrast (4:1) slanted-edges. The relatively high contrast of the Siemens Star (specified as >50:1) makes measurement results quite sensitive to clipping and nonlinearities in tonal response. Low contrast (4:1) slanted-edges closely approximate features our eyes use to perceive sharpness, and they rarely saturate the image. Measurements based on slanted-edges accurately represent real-world performance: they work extremely well for testing of cameras in wide range of applications, from product development to manufacturing.
We compare MTF calculation results from slanted-edge patterns, which are performed by Imatest SFR, SFRplus, and eSFR ISO, with results from sinusoidal patterns, which are performed by the Imatest Star chart (for the Siemens star) and Log F-Contrast modules, paying special attention to the effects of signal processing, especially sharpening and noise reduction (which are performed by software or in-camera firmware).
Most consumer cameras sharpen images in the presence of contrasty features (like edges) and reduce noise (lowpass filtering; the opposite of sharpening) in their absence. The details of this processing are more complex, or course, and vary greatly for different cameras. For this reason we tested six cameras for this report. We start by analyzing a camera whose image sensor and pixel size is between that of camera phones and DSLRs: the Panasonic Lumix LX7 (a high-end point-and-shoot with an excellent Leica zoom lens and optional raw output). We also analyze a camera phone with excessive sharpening, and in Slanted-Edge versus Siemens Star, Part 2 we show results for four additional cameras (one camera phone, one Micro Four-Thirds mirrorless camera, and two full frame DSLRs).
The images
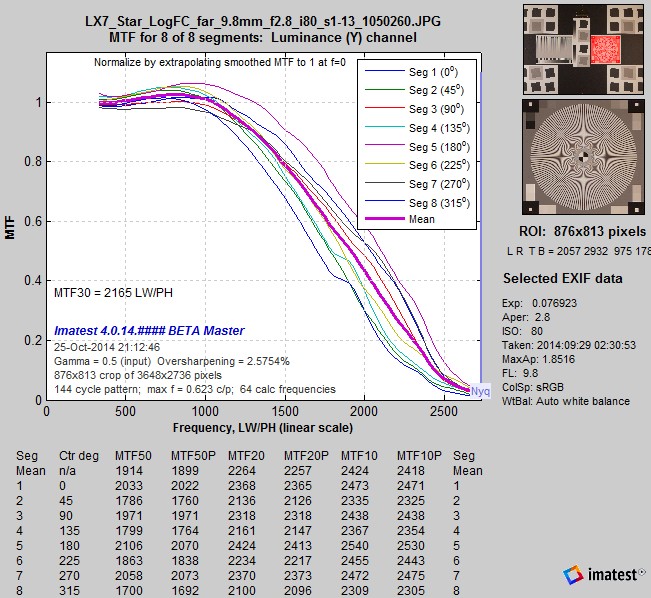
These images are from the LX-7 camera, set at f/2.8, 9.8mm focal length (50mm-equivalent). JPEG and RAW images were captured simultaneously. LX-7 JPEG images are sharpened with a radius of 1, which means the strongest sharpening boost is near the Nyquist frequency (0.5 cycles/pixel).
 SFRplus chart: 4:1 contrast slanted-edges SFRplus chart: 4:1 contrast slanted-edges(from the JPEG image) |
 Composite chart with Log F-Contrast and Star charts Composite chart with Log F-Contrast and Star chartsand slanted edges with ~12:1 and 2:1 contrast. |
Raw results
We start by comparing minimally processed images (derived from raw, with no sharpening, noise reduction, or gamma encoding) with in-camera JPEG images (highly processed) for the same image captures using for ISO speeds of 80 (the minimum) and 1600.
To obtain the minimally processed images, raw images were demosaiced and saved as TIFF files using dcraw, which applies no sharpening or noise reduction. Output gamma was set to 1.0 (Linear; i.e., no encoding gamma), White Balance was set to None, and Output color space was set to RAW. The converted raw images can be considered to be “original” (i.e., unprocessed) images.
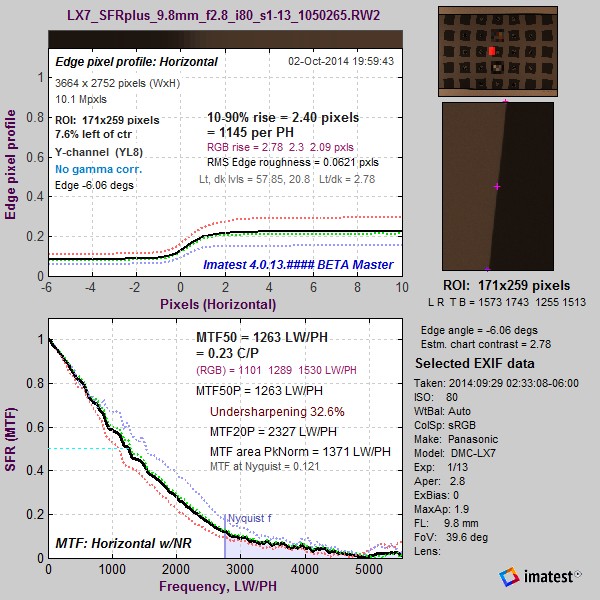 Raw image @ ISO 80; 4:1 edge Raw image @ ISO 80; 4:1 edge |
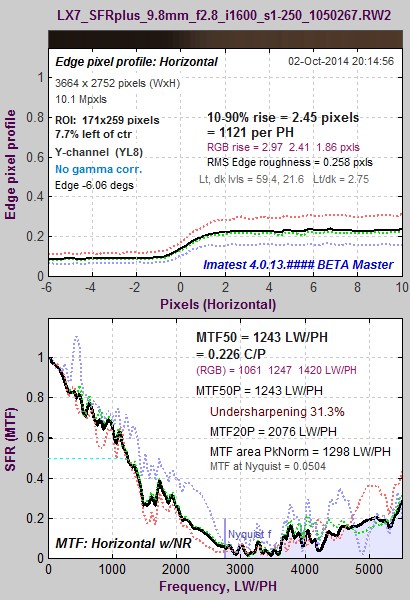 Raw image @ ISO 1600; 4:1 edge Raw image @ ISO 1600; 4:1 edge |
Comparison of these two images of the same SFRplus chart shows that the only significant effect of increasing ISO speed is to increase noise. Note that the converted raw image (with gamma = 1) is considerably darker than the JPEG image (with gamma around 0.5), shown above.
The monotonically-decreasing shape of the MTF curve (clearer on the less noisy image on the left) is characteristic of unsharpened images. Sharpened images have a characteristic boost in middle spatial frequencies (below the Nyquist frequency) described in more detail here. We will use the curves for comparison with sharpened images, below.
These two plots show that edge contrast has very little effect on MTF of raw slanted-edges. Now we look at results for the Siemens star (at several angles) and the Log F-Contrast chart (for several contrast levels).
Results are very similar to slanted-edge measurements. We don’t show ISO 1600 because it would be more of the same.
Summary— Raw MTF results are relatively independent of chart type, contrast level, and ISO speed. Their monotonically-decreasing shape is a clear indicator that no sharpening has been applied. This is not the case for (highly processed) camera JPEG images.
Slanted-edge results
The results below show how slanted-edges are affected by JPEG signal processing (especially sharpening) in the LX7, which is performed by software/firmware. Compared to the unprocessed images, rise distance is shorter; edge overshoots and undershoots are visible, and the MTF curve has a peak (as high as 1.2) around Nyquist/3– typical of moderately strong sharpening.
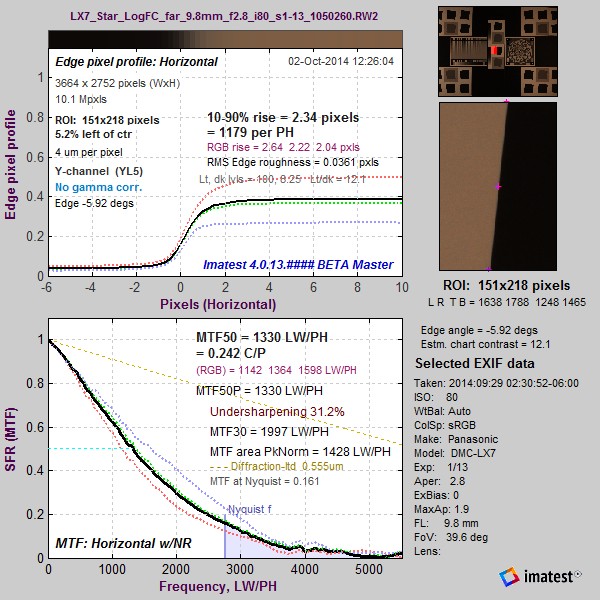
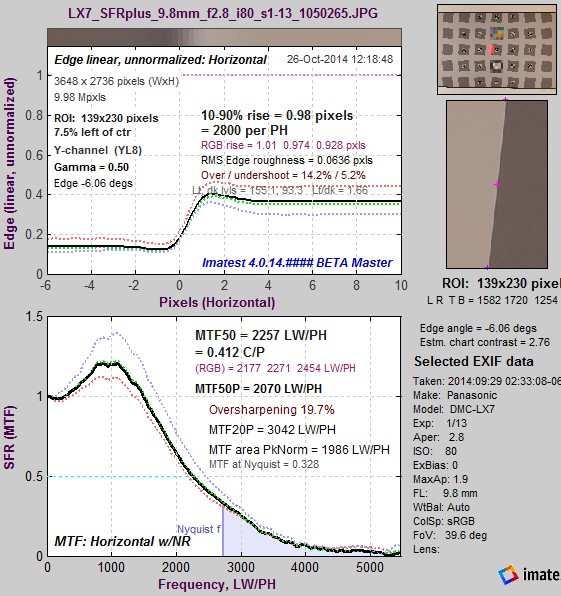 Camera JPEG @ ISO 80; 4:1 edge. Camera JPEG @ ISO 80; 4:1 edge.MTF50P = 2078 LW/PH. |
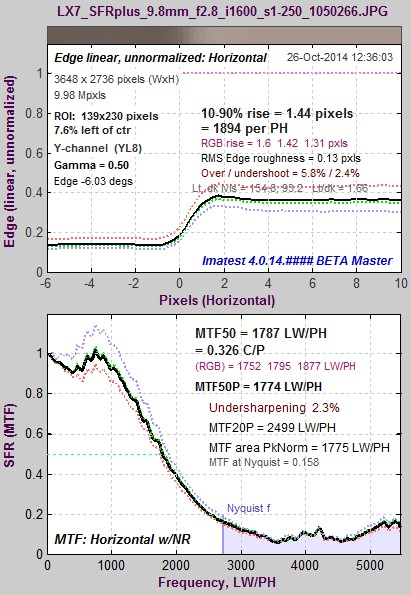 Camera JPEG @ ISO 1600; 4:1 edge. Camera JPEG @ ISO 1600; 4:1 edge.MTF50P = 1771 LW/PH. |
There is clearly less sharpening for ISO 1600 than for ISO 80. (The additional response above the Nyquist frequency is due to noise.) Note that the ratio between the light and dark regions is reduced in the JPEG image (compared to the raw image, above) because an encoding gamma has been applied.
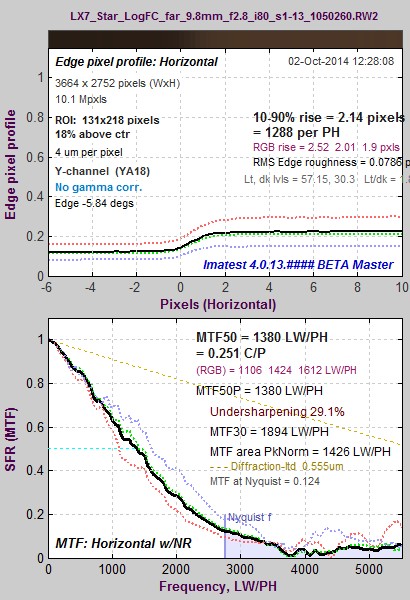
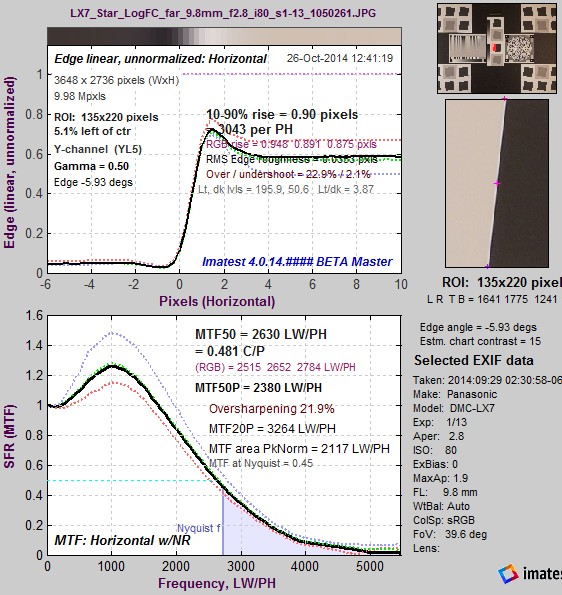 Camera JPEG @ ISO 80; ~12:1 edge. Camera JPEG @ ISO 80; ~12:1 edge.MTF50P = 2206 LW/PH. |
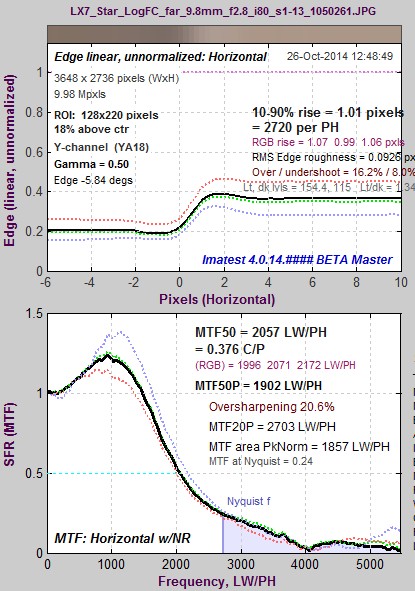 Camera JPEG @ ISO 80; 2:1 edge. Camera JPEG @ ISO 80; 2:1 edge.MTF50P = 1832 LW/PH. |
| Chart Contrast |
MTF50 (C/P) | MTF50 (LW/PH) | MTF20P (LW/PH) |
Overshoot % |
(All ISO 80) Compared to the 4:1 contrast edge, MTF50 is higher for the high contrast (~12:1) edge and is lower for the 2:1 edge; though the overshoot variation is less than some other cameras we’ve observed. This behavior is typical of consumer cameras, which tend to have more sharpening near contrasty features and less sharpening (often none at all, or noise reduction (lowpass filtering)— which is the inverse of sharpening) in the absence of contrasty features. The sharpening boost is very clear for slanted-edges. Note that LX-7 JPEG images are sharpened with a radius of 1, which means the strongest sharpening boost is near the Nyquist frequency (0.5 cycles/pixel). |
| Edge 2:1 | 0.376 | 2057 | 2703 | 16% | |
| Edge 4:1* | 0.412 | 2257 | 3042 | 14% | |
| Edge ~12:1 | 0.481 | 2630 | 3264 | 23% | |
| Log F-C maximum |
2100 | 2408 | 6% | ||
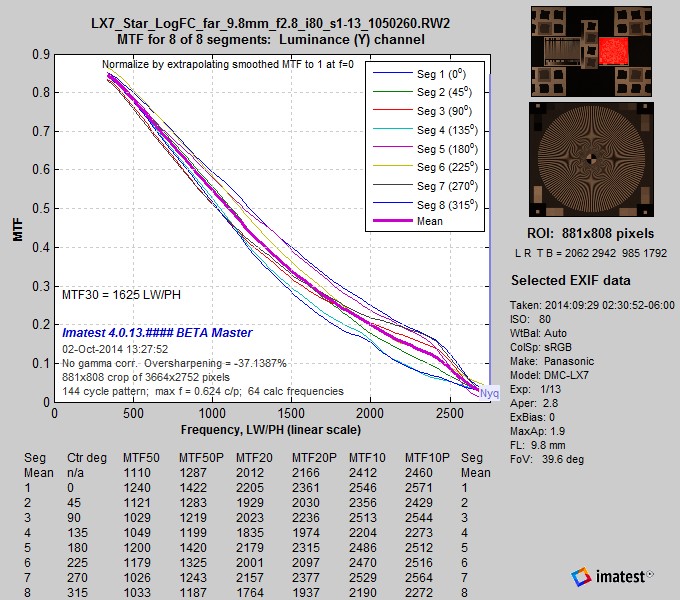
| Siemens Star mean | 1914 | 2257 |
Sinusoidal (Log F-Contrast and Siemens star) results
Both the Log F-Contrast chart and the Siemens Star have sinusoidal patterns. The Siemens Star is specified in ISO 12233:2014 Annex E as having a contrast ratio between 50:1 and 250:1 (very high!), hence we expect it to have a similar MTF response as the top (highest contrast) row of the Log F-Contrast chart. The key differences:
- The Log F-Contrast measures MTF in a single direction (horizontal), but has a range of contrast levels.
- The Siemens Star measures MTF in multiple directions, but has a single contrast level (typically high contrast).
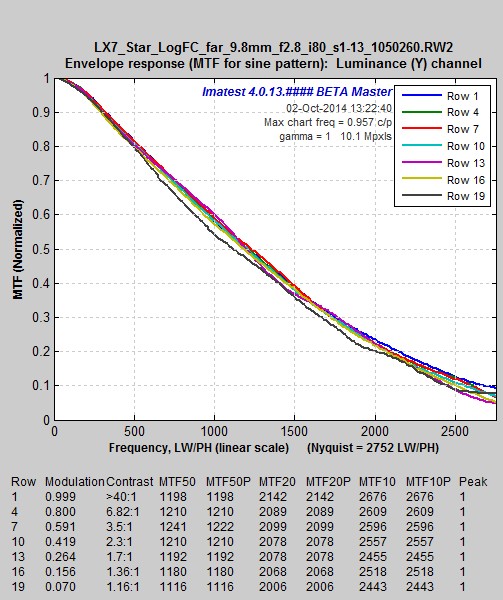
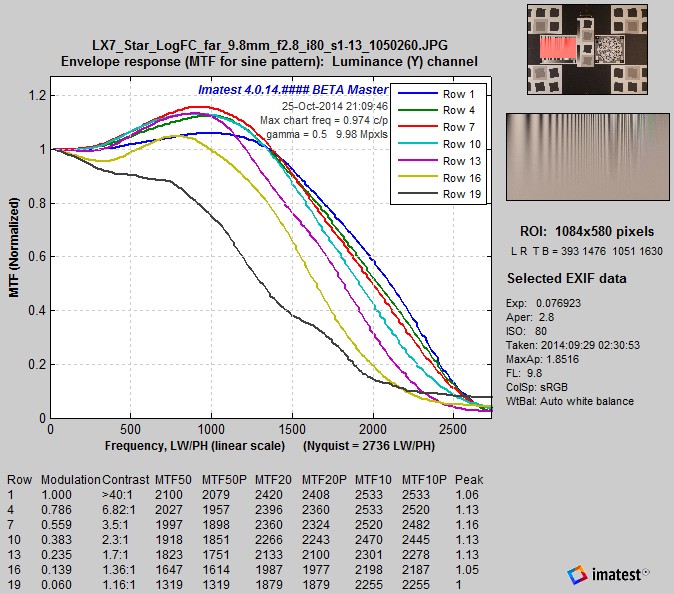 MTF for Log F-Contrast, rows 1-19 in steps of 3, MTF for Log F-Contrast, rows 1-19 in steps of 3,Camera JPEG @ ISO 80 |
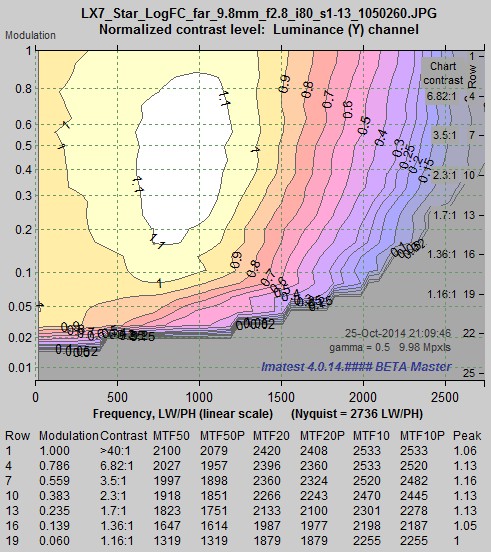 MTF contours for Log F-Contrast image, MTF contours for Log F-Contrast image,Camera JPEG @ ISO 80 |
The two plots (above) display the same MTF results for the Log F-Contrast chart in two different formats: actual MTF curves (above left) and MTF contour plots (above right). The contour plots are clearer for observing how response changes with contrast (see Sharpness and Texture Analysis using Log F‑Contrast from Imaging-Resource for a number of interesting examples), but the MTF curves are better for comparing with the Star chart results, below. Sharpening is present in rows with modulation levels greater than 0.1 (contrast > 1.25:1). It decreases very rapidly for modulation below 0.1.
A curious phenomenon is visible in these plots: sharpening decreases for the highest contrast levels. It is distinctly lower for row 1 than for rows 4-13. When we looked at the tonal response of this camera (from the grayscale pattern just below the Log F-Contrast pattern) we did not see any issues with contrast or tonal nonlinearity. It appears likely that the LX7 signal processing pipeline reduces sharpening for very high contrast levels in order to reduce the likelihood of clipping.
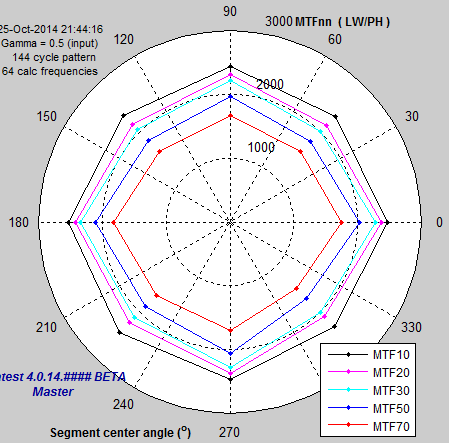
These results show that the Siemens star has a significant amount of sharpening, though somewhat less than the slanted edges.
A camera phone with extreme sharpening
In early 2013 we received images from a camera phone that had an extreme— and highly atypical— amount of sharpening. We described the results of testing this image in Dead Leaves measurement issue. We did not receive a Siemens star image, but, as we have shown, the response of Row 1 of the sinusoidal Log F-Contrast chart should be very close to the response of the (high contrast) Siemens Star. Here are the Log F-Contrast results.
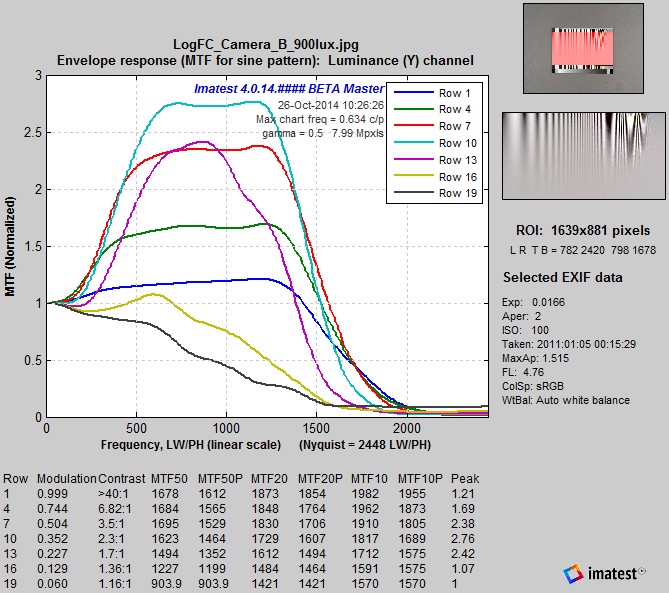 MTF for extremely sharpened image: MTF for extremely sharpened image:Log F-Contrast, rows 1-19 in steps of 3 (of 25), Camera JPEG @ ISO 100 |
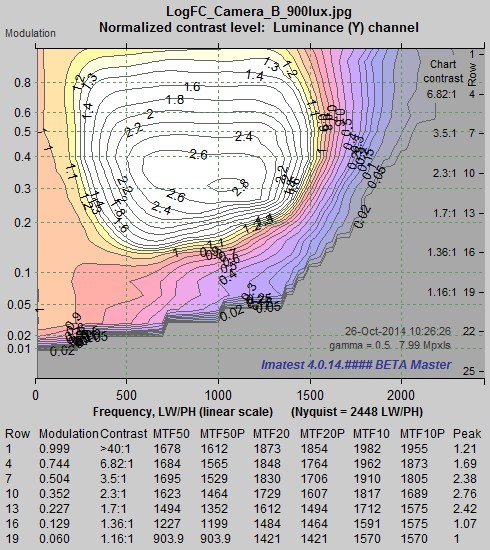 MTF contours for extremely sharpened image: MTF contours for extremely sharpened image:Log F-Contrast, Camera JPEG @ ISO 100 |
|
For this camera, the MTF of the sinusoidal Log F-Contrast chart indicates an extreme amount of sharpening. The maximum peak MTF response (2.8) occurred at the row where modulation = 0.3 (approximately 2:1 contrast). This happens because sharpening causes the upper rows of the Log F-Contrast chart to saturate, i.e., clip (go to pure white and black), which reduces the peak modulation. Saturation is visible in a crop of the image, shown on the right. Click on image to view the entire chart full-sized. Note the reduced contrast on the left of this image (for spatial frequencies below the sharpening peak). |
 Crop of extremely sharpened sinusoidal (Log F-Contrast) Crop of extremely sharpened sinusoidal (Log F-Contrast)image, showing saturation. Click on image to view full-sized. |
|
Saturation is clearly evident in the plot on the right of the original and linearized pixel levels. Row 1 (the highest contrast row on the top, equivalent to the Siemens Star, shown in cyan), is so strongly saturated that there is only a small sharpening peak. Row 7 (about 1/3 of the way down, shown in black), is also strongly saturated, but has much lower modulation at low spatial frequencies, so it’s MTF peak (relative to low spatial frequencies) is much larger (2.4, shown in the red curve, above left). Pixel pattern plot: Log F-Contrast chart, Siemens star MTF results for this camera should correspond to the dark blue curve (Row 1) in the MTF plot above, which taken by itself looks very good (low sharpening peak, excellent MTF). It is difficult to tell how misleading these results are until you view the spatial domain results. The key takeaway from this is that you cannot characterize system performance from sinusoidal charts from MTF results alone. You must also look at spatial domain results (such as the pixel plot on the right) be sure there is no saturation (which invalidates the measurements). |
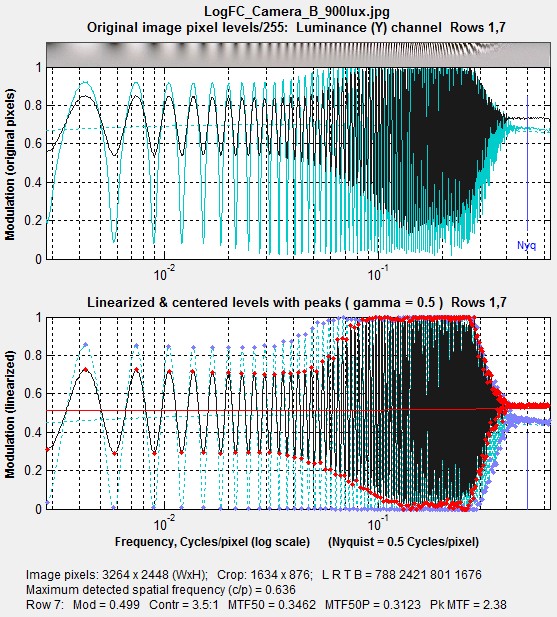 |
Summary
Our perception of image sharpness is closely correlated to the appearance of edges (contrast boundaries) in the image. This is a key reason for the use of edges in MTF measurement (the slant makes the result insensitive to sampling phase). Saturation was often a problem with the edges in the old ISO 12233:2000 chart, which had a specified minimum contrast of 40:1 (80:1 or more was commonplace). This problem was resolved in the new ISO 12233:2014 standard (released in February 2014; implemented in SFRplus and ISO 12233:2014 Edge SFR charts), which specified an edge contrast of 4:1. Not only are these edges unlikely to saturate, their contrast is similar to real-world features that affect our perception of sharpness. Measurements based on low-contrast slanted-edges accurately represent imaging system performance.
| Results from the six cameras we tested (two on this page, four in Part 2) show that MTF results for both slanted-edges and Siemens stars (as well at other sinusoidal patterns) are sensitive to sharpening (and that there tends to be more sharpening for higher contrast features, although some cameras may reduce sharpening at the very highest contrast levels). We also found that the Siemens star was more affected by saturation and non-uniform signal processing in high contrast regions. Saturation tends to flatten the Siemens star MTF response— to reduce peak MTF, making it appear that it is less sensitive to sharpening, when in fact the MTF measurement is questionable. |
The sensitivity of slanted edges to sharpening is not a drawback because it is not excessive and it represents the way we perceive image sharpness.
| Advantages | Disadvantages | |
| Slanted- Edge |
More efficient use of space (allows a detailed map of sharpness over the image surface). Faster. Robust in the presence of optical distortion. |
Slightly more sensitive to software sharpening, depending on camera firmware. Measures only near-horizontal and vertical edges. |
| Siemens Star |
Slightly less sensitive to software sharpening. Measures MTF for a variety of angles (not just near-horizontal and vertical), though these measurements seem to be affected only by demosaicing and sharpening. |
Requires more space. Slower. Saturation in highly oversharpened images is not obvious from measurement results. |
Conclusions
Our key conclusion:
| The slanted-edge pattern provides accurate and robust measurements. Its speed and efficient use of space (which allows detailed sharpness maps) makes it the best choice for measuring the performance of a wide variety of camera systems and applications, from product development to production testing. |