|
NOTE: The method in this page is obsolete and is deprecated in Imatest 2020.1. It does not produce accurate results. The new method uses the Siemens star test chart. There is also a new method for slanted-edges that is less accurate than the star method, but is somewhat interesting as an approximation. |
Nothing like a challenge! For some time I’ve been intrigued by the fact that there is such a metric for electronic communication channels— one that specifies the maximum amount of information that can be transmitted through a channel. The metric includes the effects of sharpness and noise (grain in film). And a camera— or any digital imaging system— is such a channel.
The metric, first published in 1948 by Claude Shannon* of Bell Labs, has become the basis of the electronic communication industry. It is called the Shannon channel capacity or Shannon information transmission capacity C , and has a deceptively simple equation.
\(\displaystyle C = W log_2 \left(\frac{S+N}{N}\right) = W log_2 \left(\frac{S}{N}+1\right)\)
W is the channel bandwidth, which corresponds to image sharpness, S is the signal energy (the square of signal voltage), and N is the noise energy (the square of the RMS noise voltage), which corresponds to grain in film. It looks simple enough (only a little more complex than E = mc2 ), but the details must be handled with care. Fortunately you don’t need to know the details to take advantage of the results. We present a few key points, then some results. More details are in the green (“for geeks”) box at the bottom.
*Claude Shannon was a genuine genius. The article, 10,000 Hours With Claude Shannon: How A Genius Thinks, Works, and Lives, is a great read.
Caveat: Shannon capacity is an experimental measure of perceived image quality, and is not yet a reliable measurement. Much work needs to be done to verify its validity.
Shannon capacity is NOT a trustworthy metric for JPEG files from most consumer cameras, where image processing varies over the image surface and noise reduction improves measured Signal-to-Noise Ratio while removing information.
Shannon capacity measurements can be fooled by commonplace digital signal processing. Noise reduction (lowpass filtering, i.e., smoothing, in areas that lack contrasty detail) may improve the measured signal-to-noise ratio, S/N, and hence increase C, but it removes fine, low contrast detail, i.e., it removes information. Sharpening (boosting high spatial frequencies in the vicinity of contrasty details) increases bandwidth W, but adds no information.
Please keep this in mind when you read this page and interpret Imatest results.
Meaning of Shannon capacity
In electronic communication channels the Shannon capacity is the maximum amount of information that can pass through a channel without error, i.e., it is a measure of its “goodness.” The actual amount of information depends on the code— how information is represented. But coding is not relevant to digital photography. What is important is the following hypothesis:
I stress that this statement is a hypothesis— a fancy mathematical term for a conjecture. It agrees with my experience and that of many others, but it needs more testing (with a variety of images) before it can be accepted by the industry. Now that Shannon capacity can be calculated with Imatest, we have an opportunity to learn more about it.
The Shannon capacity, as we mentioned, is a function of both bandwidth W and signal-to-noise ratio, S/N. It’s important to use good numbers for both of these parameters.
In texts that introduce the Shannon capacity, bandwidth W is usually assumed to be the half-power frequency, which is closely related to MTF50. Strictly speaking, this is only correct for white noise (a flat spectrum) and a simple low pass filter (LPF). But digital cameras have varying amounts of sharpening, and strong sharpening can result in response curves with large peaks that deviate substantially from simple LPF response.
When we started working with Shannon capacity (early in the evolution of Imatest) we attempted to get around this problem by using standardized sharpening, which sets the response at 0.3 times the Nyquist frequency equal to the response at low frequencies. MTF50C (corrected; with standardized sharpening) is used for bandwidth W. We no longer recommend this approach: because of nonuniform signal processing (strong sharpening near edges; noise reduction away from edges), processed files out of cameras (usually JPEGs) simply can’t be trusted. Raw files, which have minimal sharpening and noise reduction (and usually have uniform signal processing) are more trustworthy.
The choice of signal S presents some serious issues when calculating the signal-to-noise ratio S/N because S can vary widely between images and even within an image. It is much larger in highly textured, detailed areas than it is in smooth areas like skies. A single value of S cannot represent all situations.
To deal with this we start with a standard value of signal, Sstd: the difference between the white and black zones in a reflective surface such as the ISO 12233 test chart. This represents a tonal range of roughly 80:1 (a pixel ratio of about 9:1 for for an image encoded with gamma = 1/2: typical for a wide range of digital cameras). Then we plot Shannon capacity C for a range of S from 0.01*Sstd (representing very low contrast regions) to 2*Sstd (about a 160:1 contrast range, which represents an average sunny day scene— fairly contrasty). Imatest displays values of C for three contrast levels relative to Sstd: 100% (representing a contrasty scene), 10% (representing a low contrast scene), and 1% (representing smooth areas). Results are shown below.
Imatest results
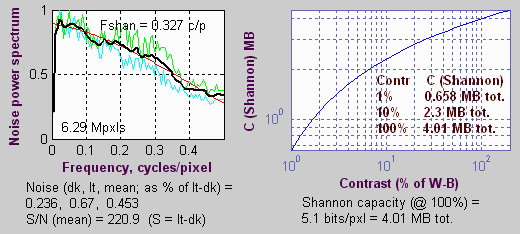
Imatest displays noise and Shannon capacity plots at the bottom of the Chromatic aberration figure if the (Plot) Shannon capacity and Noise spectrum (in CA plot) checkbox in the SFR input dialog box is checked (the default is unchecked) and the selected region is sufficiently large. Here is a sample for the Canon EOS-10D.
The noise spectrum plot is experimental. Its rolloff is strongly affected by the amount of noise reduction. The pale green and cyan lines represent two different calculation methods. The thick black line is the average of the two. The red line is a second order fit. Noise spectrum will become more meaningful as different cameras are compared.
RMS noise voltage in the dark and light areas is expressed as a percentage of the difference between the light and dark signal levels, i.e., the standard signal S = Sstd., i.e., noise is actually N/Sstd. The inverse of mean (the average of the two) is used as S/N in the equation forC.
\( C = W log_2 bigl( (S/N)^2 +1 bigr) = 3.322; W log_{10}bigl( (S/N)^2 + 1 bigr) \)
Shannon capacity C is calculated and displayed for three contrast levels.
| Contrast | Signal S | Description |
|---|---|---|
| 100% | The standard signal, S = Sstd | This is about an 80:1 contrast ratio— a moderately contrasty image. Indicates image quality for contrasty images. Weighs sharpness more heavily than noise. |
| 10% | S = Sstd /10 | Indicates image quality for low contrast images. |
| 1% | S = Sstd /100 | This represents an extremely low contrast image. Indicates image quality in smooth areas such as skies. Weighs noise more heavily. |
The values of C are meaningful only in a relative sense— only when they are compared to a range of other cameras. Here are some typical results, derived from ISO 12233 charts published on the internet.
| Camera | Pixels V x H (total Mpixels) |
MTF50 LW/PH |
MTF50C LW/PH |
S/N | ISO | C (MB) 100% |
C (MB) 10% |
C (MB) 1% |
Comments |
|---|---|---|---|---|---|---|---|---|---|
| Canon EOS-10D | 2048×3072 (6.3) | 1325 | 1341 | 221 | 100 | 4.01 | 2.30 | 0.66 | |
| Canon EOS-1Ds | 2704×4064 (11) | 1447 | 1880 | 184 | 100 | 7.18 | 4.01 | 1.02 | Little built-in sharpening. |
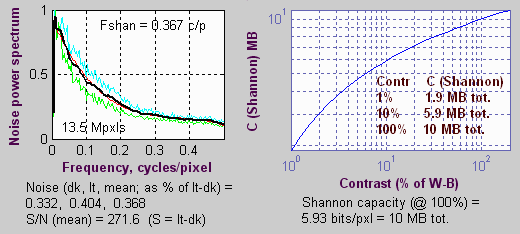
| Kodak DCS-14n | 3000×4500 (13.5) | 2102 | 2207 | 272 | 100? | 10.0 | 5.92 | 1.90 | No anti-aliasing filter. Strong noise reduction. |
| Nikon D100 | 2000×3008 (6) | 1224 | 1264 | 148 | 200? | 3.43 | 1.85 | 0.40 | |
| Nikon D70 | 2000×3008 (6) | 1749 | 1692 | 139 | ? | 4.53 | 2.42 | 0.50 | Strikingly different response from D100. Less aggressive anti-aliasing. |
| Sigma SD10 | 1512×2268 (3.4) | 1363 | 1381 | 288 | 100 | 3.20 | 1.9 | 0.63 | Foveon sensor. No anti-aliasing filter. Very high MTF50C and response at Nyquist. |
| Canon G5 | 1944×2592 (5) | 1451 | 1361 | 94 | ? | 2.89 | 1.43 | 0.20 | Strongly oversharpened. |
| Sony DSC-F828 | 2448×3264 (8) | 1688 | 1618 | 134 | 64 | 4.67 | 2.47 | 0.49 | Compact 8 MP digital with excellent lens. S/N and C are expected to degrade at high ISO. |
Performance measurements were taken from the edge located about 16% above the center of the image.
Here are some additional examples, illustrating unusual noise spectra. The Kodak DCS-14n shows a steep rolloff indicative of extreme noise reduction. This is reflected in the unusually high Shannon capacity at 1% contrast.
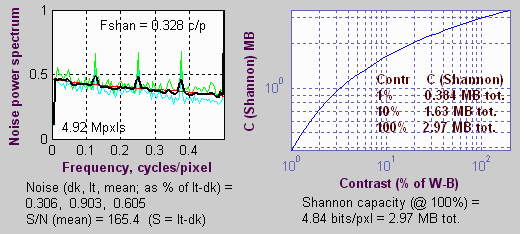
The Olympus E-1 has an unusual noise spectrum, with a spike at Nyquist. I don’t know what to make of it.
Summary
Here is a summary of the key points.
- Shannon capacity C has long been used as a measure of the goodness of electronic communication channels.
- Imatest calculates the Shannon capacity C for the Y (luminance) channel of digital images.
- The calculation of C is an approximation: it is not precise, but may be useful for comparing the performance of digital cameras (or scanned film images).
- We hypothesize that C is closely related to overall image quality; that it provides a fair basis for comparing cameras with different pixel counts, sharpening, and noise levels.
- Because of non-uniform signal processing, C calculated from camera JPEG images in not trustworthy. It is better with raw images.
- We display values of C that correspond to three signal levels, 100%, 10% and 1%, representing moderately contrasty images, low contrast images, and smooth areas.
- Shannon capacity has not been used to characterize photographic images because it was difficult to calculate and interpret. But now it can be calculated easily, its relationship to photographic image quality is open for study.
- We stress that C is still an experimental metric for image quality. Much work needs to be done to demonstrate its validity. Noise reduction and sharpening can distort its measurement. Imatest results for C should therefore be regarded with a degree of skepticism; they should not be accepted uncritically as “the truth.”
Further considerations and calculations
- Since Imatest displays S and N as voltage rather than power or energy (both of which are proportional to the square of voltage), the equation used to evaluate Shannon capacity per pixel is \(C_P = W log_2 bigl( (S/N)^2 + 1 bigr) \), where W is measured in cycles per pixel. The total capacity is \( C = C_P times text{number of pixels}\).
- Imatest calculates Shannon capacity C for the luminance channel (Y ≅ 0.3*R + 0.6*G + 0.1*B), which represents the eye’s sensitivity to the three primary colors and best represents how the eye detects information in typical scenes. C could be calculated separately for each of the channels (R, G, and B), but this would cause unnecessary confusion.
- The channel must be linearized before C is calculated, i.e., an appropriate gamma correction (signal = pixel levelgamma, where gamma ~= 2) must be applied to obtain correct values of S and N. The value of gamma (close to 2) is determined from runs of any of the Imatest modules that analyze grayscale step charts: Stepchart, Colorcheck., Multicharts, Multitest, SFRplus, or eSFR ISO.
- Digital cameras apply varying degrees of noise reduction, which may make an image look “prettier,” but removes low contrast signals at high spatial frequencies (which represent real texture information). Noise reduction makes the Shannon capacity appear better than it really is, but it results in a loss of information— especially in low contrast textures— resulting in images where textures look “plasticy” or “waxy.” The exact amount of noise reduction cannot be determined with a simple slanted-edge target (especially with JPEG images from cameras). The Log Frequency-Contrast chart and module provides some information on noise reduction vs. image contrast, but is not easy to apply to the Shannon capacity calculation. Noise reduction results in an unusually rapid dropoff the noise spectrum— which is evident when several cameras are compared (demosaicing alone typically cause the noise spectrum to drop by half at the Nyquist freqnency). For all these reasons we recommend working with raw images when possible.
Because of a number of factors (noise reduction, the use of MTF50C to approximate W, the arbitrary nature of S, etc.) the Shannon capacity calculated by Imatest is an approximation. But it can be useful for comparing different cameras.
Calculating Shannon capacity
The measurement of Shannon capacity is complicated by two factors.
- The voltage in the image sensor is proportional to the energy (the number of photons) striking it. Since Shannon’s equations apply to electrical signals, I’ve stuck to that domain.
- The pixel level of standard digital image files is proportional to the sensor voltage raised to approximately the 1/2 power. This is the gamma encoding, designed to produce a pleasing image when the luminance of an output device is proportional to the pixel level raised to a power of 2.2 (1.8 for Macintosh). This exponent is called the gamma of the device or the image file designed to work with the device. Gamma = 2.2 for the widely-used sRBG and Adobe RGB (1998) color spaces. Since I need to linearize the file (by raising the pixel levels to a power of 2) to obtain a correct MTF calculation, I use the linearized values for calculating Shannon capacity, C.
The correct, detailed equation for Shannon capacity was presented in Shannon’s second paper in information theory, “Communication in the Presence of Noise,” Proc. IRE, vol. 37, pp. 10-21, Jan. 1949.
\(displaystyle C_1 = int_0^W log bigl( 1 + frac{P(f)}{N(f)} bigr) df\)
W is maximum bandwidth, P(f) is the signal power spectrum (the square of the MTF) andN( f ) is the noise power spectrum. There are a number of difficulties in evaluating this integral. Because P and N are calculated by different means, they are scaled differently. P(f) is derived from the Fourier transform of the derivative of the edge signal, while N( f ) is derived from the Fourier transform of the signal itself. And noise reduction removes information while reducing N( f ) at high spatial frequencies below its correct value. For this reason, until we solve the scaling issues we use the simpler, less accurate, but less error-prone approximation,
\( C = W log_2 bigl( (S/N)^2 + 1 bigr) \)
where bandwidth W is traditionally defined as the channel’s -3 dB (half-power) frequency, which corresponds to MTF50,S is standard (white - black) signal voltage, andN is RMS noise voltage. The square term converts voltage into power. S/N (the voltage signal-to-noise ratio) is displayed by Imatest. (S/N can refer to voltage or power in the literature; you have to read carefully to keep it straight.)
Strictly speaking, this approximation only holds for white noise and a fairly simple (usually second-order) rolloff. It holds poorly when P( f ) has large response peaks, as it does in oversharpened digital cameras. The standardized sharpening algorithm comes to the rescue here. Imatest uses MTF50C (the 50% MTF frequency with standardized sharpening) to approximate W. This assures that P( f ) rolls off in a relatively consistent manner in different cameras: it is an excellent relative indicator of the effective bandwidth W.
RMS (root mean square) noise voltage N is the standard deviation (sigma) of the linearized signal in either smooth image area, away from the edge. It is relatively easy to measure using the slanted edge pattern because the dynamic range of digital cameras is sufficient to keep the levels for the white and black regions well away from the limiting values (pixel levels 0 and 255). Typical average (mean) pixel values are roughly 18-24 for the dark region and 180-220 for the light region, depending on exposure. Imatest uses the average of the noise in the two regions to calculate Shannon capacity. It displays noise as N/S: normalized to (divided by) the difference between mean linearized signal level of the white and black regions, S.
Noise power N doesn’t tell the whole story of image quality. Noise spectral density plays an important role. The eye is more sensitive to low frequency noise, corresponding to large grain clumps, than to high frequency noise. To determine the precise effect of grain, you need to include its spectral density, the degree of enlargement, the viewing distance, and the MTF response of the human eye. High frequency noise that is invisible in small enlargements may be quite visible in big enlargements. Noise metrics such as Kodak’s print grain index, which is perceptual and relative, takes this into account. Fortunately the noise spectrum of digital cameras varies a lot less than film. It tends to have a gradual rolloff (unless significant noise reduction is applied), and remains fairly strong at the Nyquist frequency. It’s not a major factor in comparing cameras— the RMS noise level is far more important.
Very geeky: The limiting case for Shannon capacity. Suppose you have an 8-bit pixel. This corresponds to 256 levels (0-255). If you consider the distance of 1 between levels to be the “noise”, then the S/N part of the Shannon equation is log2(1+2562) ˜ 16. The maximum possible bandwidth W— the Nyquist frequency— is 0.5 cycles per pixel. (All signal energy above Nyquist is garbage— disinformation, so to speak.) So C = W log2(1+(S/N)2) = 8 bits per pixel, which is where we started. Sometimes it’s comforting to travel in circles.
History
R. Shaw, “The Application of Fourier Techniques and Information Theory to the Assessment of Photographic Image Quality,” Photographic Science and Engineering, Vol. 6, No. 5, Sept.-Oct. 1962, pp.281-286. Reprinted in “Selected Readings in Image Evaluation,” edited by Rodney Shaw, SPSE (now SPIE), 1976.
Links
The University of Texas Laboratory for Image & Video Engineering is doing some interesting work on image and video quality assessment. They approach the problem using information theory, natural scene statistics, wavelets, etc. Challenging material!
Wikipedia – Shannon Hartley theorem has a frequency dependent form of Shannon’s equation that might be applicable to Imatest.
\(displaystyle C=int_0^B log_2 left( 1 + frac{S(f)}{N(f)} right) df\)

