Year: 2021
Imatest not vulnerable to Apache log4j security compromise
Security researchers disclosed the following vulnerabilities in the Apache Log4j Java logging library: CVE-2021-44228: Apache Log4j2 JNDI features do not […]
Test Chart Life Span
Best storage practices would be in a clean, dark, dry area at (~ 23°C / 72°F) or below. Exposure to UV will break […]
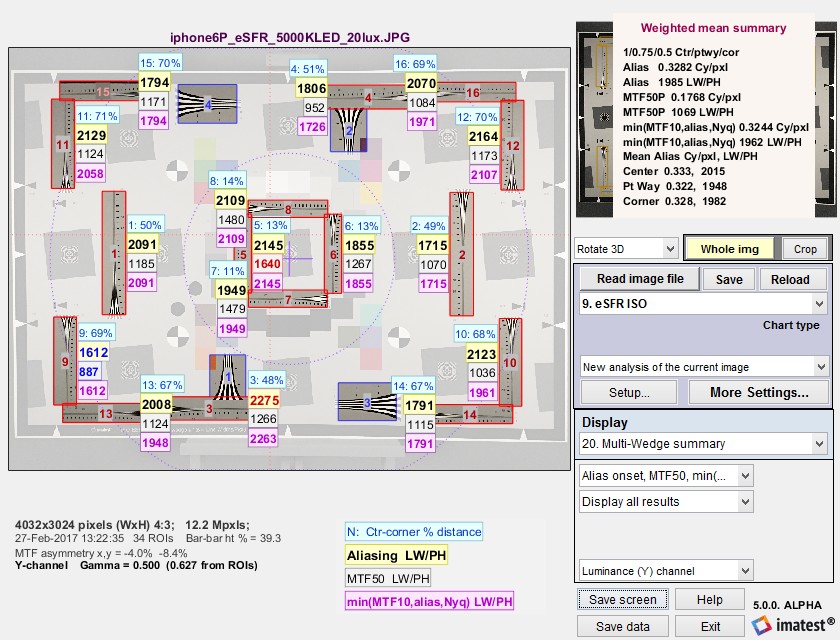
Logarithmic wedges: a superior design
We introduce the logarithmic wedge pattern, which has several advantages over the widely-used hyperbolic wedges found in ISO 12233 (current […]
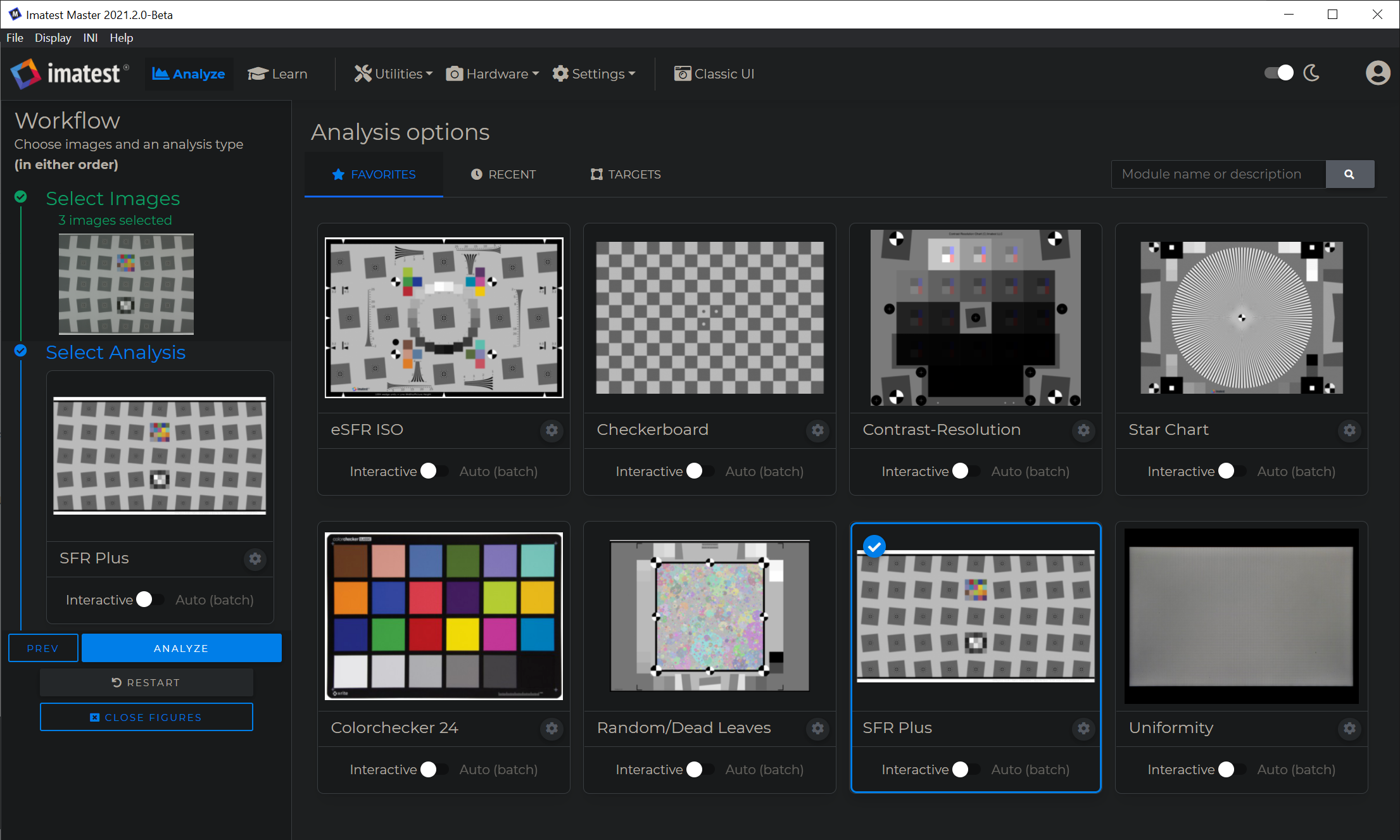
Imatest Releases Version 2021.2
Imatest Version 2021.2 introduces our new Main Window User Interface, File First Workflow, Dark Mode, a new ‘Learn’ Function, Distortion […]
How to compute resolution in TV Lines (TVL)
Television Lines (TVL) are derived from the EIA 1956 testing standard, where they are defined as the number of light and […]
Interactive vs. Auto(Batch) Analyses
Imatest has two types of analysis module: Fixed (in the left-most column of the main window) and Interactive (in the second column). Fixed modules require that […]
Camera to Chart Alignment
Centering test charts is critical for image quality testing. If the camera is not properly aligned with the test chart, […]
Long Range Testing with the OSCM10120 Target Projection Collimator
Introducing the CM10120 Collimator – a target projection collimator system that allows users to simulate long-range testing in confined spaces. […]
Using images of noise to estimate image processing behavior for image quality evaluation
In the 2021 Electronic Imaging conference (held virtually) we presented a paper that introduced the concept of the noise image, […]
Comparing sharpness in cameras with different pixel count
Introduction – Spatial frequency units – Summary metrics – Sharpening Example – Summary Introduction: The question We frequently receive questions […]
Imatest launches Subscription Software License
Imatest is excited to announce a new subscription option for all of our software products. Beginning June 1, 2021, […]
Imatest launches Camera Geometric Calibration Validation Service for ADAS and Autonomous Vehicle companies
Imatest, LLC, a leader in image quality evaluation tools, today announced the launch of their new Camera Geometric Calibration Validation […]
Imatest sells exclusive license for intrinsic geometric calibration software to Furonteer
Imatest, LLC, a leader in image quality testing software, analysis, test charts, and test lab equipment, and Furonteer, the forerunner […]
Imatest Releases Version 2021.1
Imatest Version 2021.1 adds several new features to Imatest Master and Imatest IT, including edge tracking during live focusing, alignment […]
Calculating Exposure Quality Loss per IEEE CPIQ v2
For more about Imatest’s CPIQ support click here
Imatest Founder Norman Koren Receives Lifetime Achievement Award
Imatest LLC Chief Technical Officer and Founder Norman Koren was awarded a Lifetime Achievement Award by AutoSens during the latest AutoSense-Detroit.