Author: norman
Image Processing for Image Information Metrics
The basic premise of this work is that Information capacity is a superior metric for predicting the performance of […]
Interpolated slanted-edge SFR (MTF) calculation
Introduction – The problem and its solution – working with the interpolated algorithm – Identifying the problem – Image comparisons […]
Fixed versus Interactive modules
Imatest has two types of analysis module: Fixed (in the left-most column of the Imatest main window) and Interactive (in […]
Detecting traffic lights with RCCB sensors
RCCB (Red-Clear-Clear-Blue) sensors are widely used in the automotive industry because their sensitivity and Signal-to-Noise Ratio (SNR) is better than […]
Scene-referenced noise and SNR for Dynamic Range measurements
The problem — in the post on Dynamic Range (DR), DR is defined as the range of exposure, i.e., scene […]
Logarithmic wedges: a superior design
We introduce the logarithmic wedge pattern, which has several advantages over the widely-used hyperbolic wedges found in ISO 12233 (current […]
Comparing sharpness in cameras with different pixel count
Introduction – Spatial frequency units – Summary metrics – Sharpening Example – Summary Introduction: The question We frequently receive questions […]
Real-time focusing with Imatest Master direct data acquisition
Speed up your testing with real-time focusing in Imatest Master 2020.2. Recent speed improvements allow for real-time focusing and allow […]
Making Dynamic Range Measurements Robust Against Flare Light
Introduction A camera’s Dynamic Range (DR) is the range of tones in a scene that can be reproduced with adequate […]
Correcting nonuniformity in slanted-edge MTF measurements
Slanted-edge regions can often have non-uniformity across them. This could be caused by uneven illumination, lens falloff, and photoresponse nonuniformity […]
Measuring temporal noise
Two temporal noise methods | Results | Temporal noise image Related pages: Flatfield Statistics based on EMVA-1288 | Using Flatfield, […]
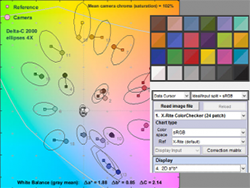
Color difference ellipses
Starting with Imatest 4.2, Imatest’s two-dimensional color displays— CIELAB a*b*, CIE 1931 xy chromaticity, etc.— in Multicharts, Multitest, Colorcheck, SFRplus, and eSFR ISO can display ellipses that assist in visualizing perceptual color differences. You can select between MacAdam ellipses (of historical interest), or ellipses for ΔCab (familiar but not accurate), ΔC94, and ΔC00 (recommended).
SFRreg: SFR from Registration Marks
Imatest SFRreg performs highly automated measurements of sharpness (expressed as Spatial Frequency Response (SFR), also known as Modulation Transfer Function […]
Measuring Multiburst pattern MTF with Stepchart
Measuring MTF is not a typical application for Stepchart— certainly not its primary function— but it can be useful with […]
LSF correction factor for slanted-edge MTF measurements
A correction factor for the slanted-edge MTF (Edge SFR; E-SFR) calculations in SFR, SFRplus, eSFR ISO, SFRreg, and Checkerboard was […]
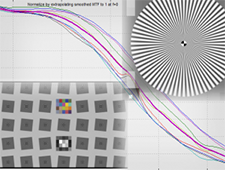
Slanted-Edge versus Siemens Star: A comparison of sensitivity to signal processing
This post addresses concerns about the sensitivity of slanted-edge patterns to signal processing, especially sharpening, and corrects the misconception that […]
Sharpness and Texture Analysis using Log F‑Contrast from Imaging-Resource
Imaging-resource.com publishes images of the Imatest Log F-Contrast* chart in its excellent camera reviews. These images contain valuable information about […]
Measuring Test Chart Patches with a Spectrophotometer
Using Babelcolor Patch Tool or SpectraShop 4 This post describes how to measure color and grayscale patches on a variety of […]
Region Selection bug workaround
Symptoms of problem: Upon selection of a region of interest, program stops working, either not responding or crashing. DOS window […]
Microsoft Lync Logo selects Imatest
Imatest is the standard test software used in the recently published Microsoft USB peripheral requirements specification entitled “Optimized for Microsoft […]